In the 2015 science fiction film, The Martian, NASA astronaut Mark Watney (Matt Damon) finds himself stranded on Mars after being struck by debris during a forced evacuation. Left for dead, the intrepid astronaut must not only survive on the barren planet, he needs to find a way home. Mark must use every resource at his disposal. We see in the TeXnical Designs article, Mark could have used LaTeX to create an ASCII table instead of rummaging through Beth Johanssen's (Kate Mara) laptop.
To communicate with NASA, Mark needs to find his way to Pathfinder, the robotic spacecraft launched in December, 1997 to explore the planet's surface. Once he acquires the probe, he can use its antenna to send a signal to NASA. Mark must travel some 800 kilometers from his HAB to Ares Vallis. Mark's rover can travel a distance of 35 km on flat terrain on full charge. Mars is really cold and, as a result, half of that power goes to the vehicle's heater. Without it, Mark can double his range. Now if only Mark had another heat source that would not draw on his vehicle's power reserves. Turns out he does. Mark has access to a radioisotope thermoelectric generator. How much of the science does the book and the movie get right?
A Big Box of Plutonium
Mark's solution, as he puts if, is to use a big box of plutonium. In this case, that big box is known as a radioisotope thermoelectric generator or RTG. The RTG generates electricity from the heat of a decaying radioactive substance, in this case, plutonium-238. This element is incredibly unstable. The nucleus breaks apart and emits radiation in the form of alpha particles or high-speed helium particles. As the alpha particles leave the plutonium nucleus, they slam into other nearby atoms and lose kinetic energy This lost energy is converted to heat. So much kinetic energy is lost that the plutonium gets red all by itself. As you guessed, Mark needs to be very careful. Any material that can fry an egg with radiation is kind of dangerous!

The Mars Science Laboratory’s radioisotope power system was assembled by putting nuclear heat sources within graphite impact shells into high-strength carbon-carbon modules at Idaho National Laboratory.
The RTG is not a nuclear reactor; it can not be controlled and its radiation output can not be increased or decreased. Everything happens naturally at the atomic level. Fortunately for Mark, it does not take much shielding to stop alpha-particles. Because of their large atomic mass, alpha particles are easily stopped by matter and can only travel a few centimeters in air. They can be absorbed by something as thin as tissue paper, or the outer layers of human skin -- which is approximately 40 micrometers thick, the equivalent of a few cells deep. Mark's RTG contains about 2.6 kilograms of plutonium and generates 1500 Watts of heat. Thermocouples positioned around the device convert 100 Watts of that heat into electricity.
This does not mean Mark should stop worrying. Pu-238 is still pretty dangerous. There is a reason why NASA does not want to put its astronauts next to glowing balls of death! While alpha particles cannot penetrate skin, ingesting or inhaling plutonium can travel deep into the body to irradiate internal organs. The element is accumulated in the liver and skeleton and becomes concentrated in those organs.
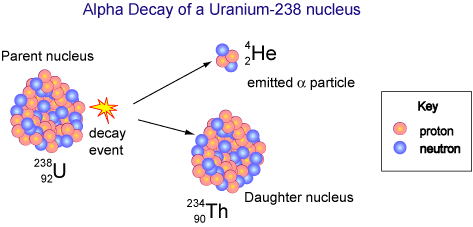
The unstable uranium-238 nucleus decays into a thorium nucleus and an alpha particle. The high-speed alpha particle loses kinetic energy and is converted to heat. Image credit: © Copyright CSIRO Australia 2004, via http://outreach.atnf.csiro.au/.
Fortunately for Mark, each plutonium pellet is sealed and insulated in graphite to prevent radiation leakage. Even if the seal is ruptured, Mark should be safe as long as he takes precautions to not breathe or ingest any radioactive particles.
Checking the Martian
While the RTG does not play as big a role in the movie as it does in the book, the science and calculations are pretty spot on. One of the devices Mark needs to survive the journey home is the atmospheric regulator. This device maintains the ratio of gasses in the air.
The atmospheric regulator uses freeze-separation to sort and store gases. Each gas has its own liquefaction or condensation point - the temperature at which a gas changes to a liquid. Cool a gas to minus 183 degrees Celcius (-297 degrees Fahrenheit) and oxygen turns to a liquid leaving nitrogen behind. If Mark needs more oxygen, the regulator can just warm up some of the liquid oxygen it has stored.
Heating up a liquid gas takes a lot of energy. Mark could let the air warm up on its own inside his rover's cabin, but the freezing cold liquid would extract all the heat from the cabin and Mark would freeze to death. Mark really does not have much energy to spare so he turns to the RTG instead of draining his rover's batteries.
In the book, Mark creates a heat reservoir by submerging the RTG in a container of water. This warms the water up. Mark can now bubble the cold sub-freezing air through the warm water to raise its temperature. Thankfully, the RTG produces 1,400 Watts of heat, giving Mark the energy he needs to survive his long trip.
In the book, Mark submerges the RTG in 20 liters or 20 kilograms of water. The specific heat capacity of water ( ), the energy required to raise one kilogram of water by one degree is
), the energy required to raise one kilogram of water by one degree is  . We can use this to calculate the rate the water temperature rises.
. We can use this to calculate the rate the water temperature rises.
The energy needed to raise the water's temperature is given by:

where  is the power input,
is the power input,  is the mass of the water,
is the mass of the water,  the specific heat capacity,
the specific heat capacity,  is the temperature, and
is the temperature, and  is the time. Solving for
is the time. Solving for  will give us the rate at which the water temperature rises. According to the book, this should be one degree per second.
will give us the rate at which the water temperature rises. According to the book, this should be one degree per second.
This becomes:

Solving for  , we get
, we get
\begin{align*}
\frac{dT}{dt} &= \frac{750}{41813} \textrm{K}\textrm{s}^{-1} \\
&= \frac{750 \times 60}{4183} \textrm{K}\, \textrm{min}^{-1} \\
&= 1.004 \textrm{K}\, \textrm{min}^{-1}
\end{align*}
That is exactly what the book described. Looks like the book got the science right! Who said putting real science into a story can't be exciting.
Also published on Medium.





